【答案】60�;18.
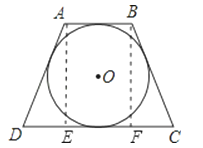
【解析】試題分析: (1)作AB⊥CD于E,BF⊥CD與F,因為⊙O為等腰梯形ABCD的內(nèi)切圓,
根據(jù)切線長定理可得:AB+CD=AD+BC=20,因為AB∥CD,所以AE=6,所以等腰梯形ABCD的面積=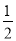 (AB+CD)AE=
(AB+CD)AE=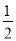 ×20×6=60,
×20×6=60,
(2)在Rt△ADE中,因為AD=10,AE=6,根據(jù)勾股定理可得DE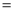 8,因為梯形ABCD為等腰梯形,
8,因為梯形ABCD為等腰梯形,
所以CF=DE=8,根據(jù)(1)中AB+CD=20,AB=EF,所以8+8+2EF=20,解得EF=2,所以梯形的下底CD=8+2+8=18.
試題解析:作AB⊥CD于E,BF⊥CD與F,如圖,
∵⊙O為等腰梯形ABCD的內(nèi)切圓,
∴AB+CD=AD+BC=20,
∵AB∥CD,
∴AE=6,
∴等腰梯形ABCD的面積=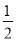 (AB+CD)AE=
(AB+CD)AE=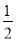 ×20×6=60,
×20×6=60,
在Rt△ADE中,
∵AD=10,AE=6,
∴DE=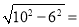 8,
8,
∵梯形ABCD為等腰梯形,
∴CF=DE=8,
而AB+CD=20,AB=EF,
∴8+8+2EF=20,解得EF=2,
∴梯形的下底CD=8+2+8=18.