
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧湱鈧懓瀚崳纾嬨亹閹烘垹鍊炲銈嗗笂缁€渚€宕滈鐑嗘富闁靛牆妫楁慨褏绱掗悩鍐茬伌闁绘侗鍣f慨鈧柕鍫濇閸樻捇鏌℃径灞戒沪濠㈢懓妫濆畷婵嗩吋閸℃劒绨婚梺鍝勫€搁悘婵嬵敂椤愩倗纾奸弶鍫涘妽瀹曞瞼鈧娲樼敮鎺楋綖濠靛鏁勯柦妯侯槷婢规洟姊洪崨濠勭細闁稿孩濞婇幆灞解枎閹惧鍘遍梺鍝勬储閸斿矂鎮橀悩鐢电<闁绘瑢鍋撻柛銊ョ埣瀵濡搁埡鍌氫簽闂佺ǹ鏈粙鎴︻敂閿燂拷婵犵數濮烽弫鍛婃叏閻戣棄鏋侀柛娑橈攻閸欏繘鏌i幋锝嗩棄闁哄绶氶弻鐔兼⒒鐎靛壊妲紒鎯у⒔缁垳鎹㈠☉銏犵闁哄啠鍋撻柛銈呯Ч閺屾盯濡烽鐓庘拻闂佽桨绀佸ú顓㈠蓟閺囷紕鐤€闁哄洨鍊妷锔轰簻闁挎棁顕у▍宥夋煙椤旂瓔娈滅€规洘顨嗗鍕節娴e壊妫滈梻鍌氬€风粈渚€骞夐垾瓒佹椽鏁冮崒姘憋紱婵犮垼鍩栭崝鏇㈠及閵夆晜鐓熼柟閭﹀枛閸斿鏌嶉柨瀣伌闁诡喖缍婇獮渚€骞掗幋婵愮€虫繝鐢靛仜閹冲繘宕濆▎鎾宠摕闁绘梻鍘х粈鍕煏閸繃顥滄い蹇ユ嫹
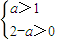 ?1<a<2
?1<a<2

